Big O Notation

What is big O notation

big o notation is used to analyze the efficiency of an algorithm: as the size of the input growth, how drastically do the space or time requirements grow with it.

So when evaluating an algorithm efficiency we must taking to consideration the efficiency of each step within the algorithm. Then find the step that has the worst performance and prioritize it over all of the better performing steps.

$O(1)$

A constant is any step that doesn’t scale with the input to the function.

$O(n^2)$ / $O(n^3)$

function Square(n) {
  for (let i = 0; i < n; i++) {
    for (let j = 0; j < n; j++) {
      for (let k = 0; k < n; k++) {
        console.log(i, j, k);
      }
    }
  }
}

$O(log n)$

function logFunc(n) {
  if (n === 0) return 'Done';
  n = Math.floor(n / 2);
  return logFunc(n);
}

function logn(n) {
  while (n < 1) {
    n = Math.floor(n / 2);
  }
}

The input n is always divided by 2, so the complexity is $O(log_{2}n)$. So if n is always divided a constant number x, it will be $O(log_{x}n)$

Binary Search

Searching must be an ordered array Thinking we need to find a certain number in this array.

1. find the midpoint of our array
2. figure out if the number we’re searching for is grater than or less than midpoint
3. if it’s greater than our number, the left array is the right side of the midpoint. Otherwise the right array
4. recur the step 1 to 3 in the left array.

function BinarySearch(arr, target, start, end) {
  if (start > end) return `Can't get it`;

  const mid = Math.floor(start + end / 2);
  if (target === arr[mid]) return `Get index ${mid}`;

  if (target > arr[mid]) return BinarySearch(arr, target, mid + 1, end);
  else return BinarySearch(arr, target, 0, mid - 1);
}

$O(nlog n)$

function nLogNFunc(n) {
  let y = n;
  while (n > 1) {
    n = Math.floor(n / 2);
    for (let i = 2; i <= y; i++) {
      console.log(i);
    }
  }
}

top loop $O(log2n)$. Inner loop keep the origin value of n so it’s $O(n)$. Totally, it’s $O(nlog_{2}n)$

Merge Sort

function MergeSort(arr) {
  if (arr.length < 2) {
    return arr;
  }
  const mid = Math.floor(arr.length / 2);

  return Merge(MergeSort(arr.slice(0, mid)), MergeSort(arr.slice(mid, arr.length)));
}

function Merge(left, right) {
  const result = [];
  let leftIndex = 0;
  let rightIndex = 0;

  while (leftIndex < left.length && rightIndex < right.length) {
    if (left[leftIndex] < right[rightIndex]) {
      result.push(left[leftIndex]);
      leftIndex++;
    } else {
      result.push(right[rightIndex]);
      rightIndex++;
    }
  }
  return [...result, ...left.slice(leftIndex), ...right.slice(rightIndex)];
}

Consider we have 4 length array, MergeSort() have two level $O(logn)$ . For EVERY LEVEL, Merge() touch each number in the array n times $O(n)$. So it’s $O(nlogn)$ totally

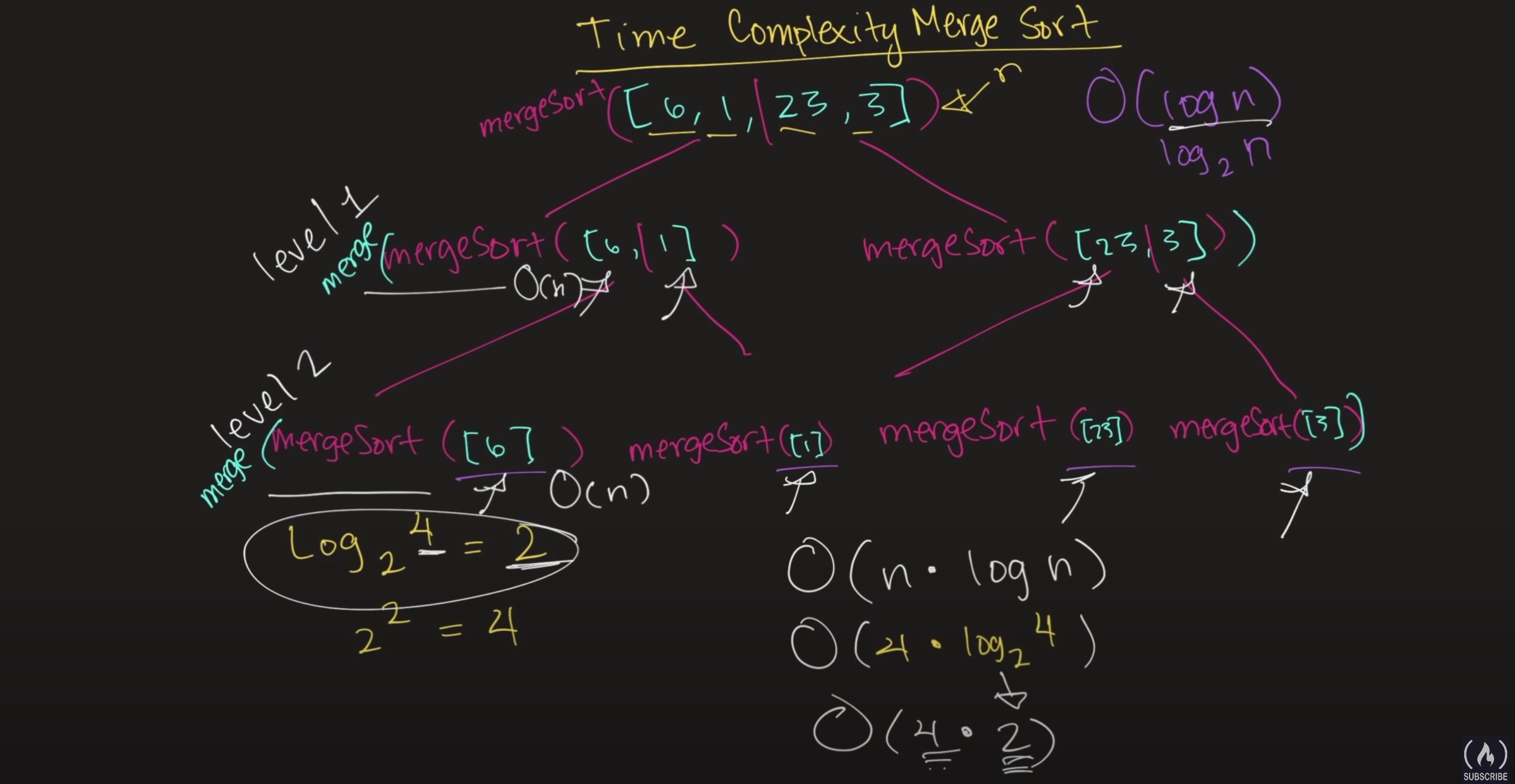
$O(2^n)$

Fibonacci

function fib(n) {
  if (n == 0) return 0;
  if (n == 1) return 1;

  return fib(n - 1) + fib(n - 2);
}

$O(n!)$

function fn(n) {
  if (n == 0) {
    return;
  }

  for (let i = 0; i < n; i++) {
    fn(n - 1);
  }
}

• 本文作者： 七渡浔
• 本文链接： https://kristineq.github.io/2022/10/06/BIG O NOTATION/
• 版权声明： 本博客所有文章除特别声明外，均采用 MIT 许可协议。转载请注明出处！